13. shadow/reflect指示文

科学技術計算でよく現れる計算パターンであるステンシル計算では，配列要素a[i]の計算のために，その周辺の値であるa[i-1]やa[i+1]などを参照します． もしa[i]がノードの担当領域の境界である場合，a[i+1]は隣接している他のノードが持っています．

a[i]を計算する度にa[i+1]を隣接ノードからコピーするのは効率が悪いので，ノードの担当領域をあらかじめ拡張しておき， ステンシル計算を行う前に隣接ノードが持っているa[i+1]をその拡張された領域にコピーすることにより， 効率的なステンシル計算を行うことを考えます． XMPでは，その拡張された領域を「袖」または「シャドウ」と呼びます．

13.1. 袖領域の宣言

13.1.1. 上界と下界で同じ袖幅を持つ場合

袖の宣言にはshadow指示文を使います． 下記の例では，分散配列aは下界と上界に1つずつ袖を持つことを宣言しています．

  • XMP/Cプログラム
#pragma xmp nodes p[4]
#pragma xmp template t[16]
#pragma xmp distribute t[block] onto p
double a[16];
#pragma xmp align a[i] with t[i]
#pragma xmp shadow a[1]
  • XMP/Fortranプログラム
!$xmp nodes p(4)
!$xmp template t(16)
!$xmp distribute t(block) onto p
real :: a(16)
!$xmp align a(i) with t(i)
!$xmp shadow a(1)
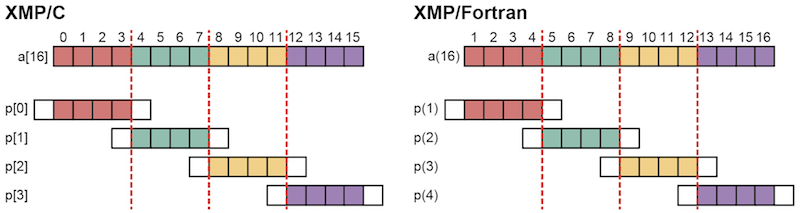
_images/shadow.png

上図においては，色のついた要素は各ノードが持っている分散配列で，白色の要素は袖になります．

注釈

cyclic分散された配列は袖を持つことはできません．

13.1.2. 上界と下界で異なる袖幅を持つ場合

プログラムによっては，上界と下界で異なる袖幅を持った方が自然な場合があります． また，上界と下界のどちらかしか袖を持っていないこともあります． 下記の例では，分散配列aは上界のみ1つの袖を持つことを宣言しています．

  • XMP/Cプログラム
#pragma xmp nodes p[4]
#pragma xmp template t[16]
#pragma xmp distribute t(block) onto p
double a[16];
#pragma xmp align a[i] with t[i]
#pragma xmp shadow a[0:1]
  • XMP/Fortranプログラム
!$xmp nodes p(4)
!$xmp template t(16)
!$xmp distribute t(block) onto p
real :: a(16)
!$xmp align a(i) with t(i)
!$xmp shadow a(0:1)
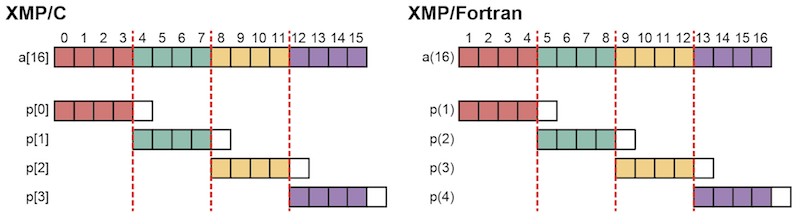
_images/shadow_uneven.png

コロン左は下界の袖数，コロン右は上界の袖数を指定します．

13.2. 袖領域の更新

13.2.1. 一般的な場合

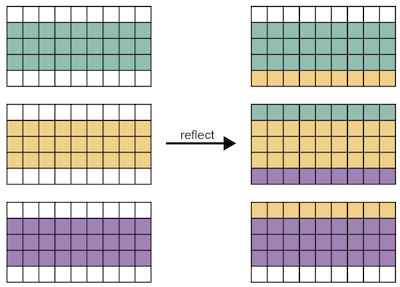
袖領域に隣接ノードが持つ値をコピーするには，reflect指示文を使います． 下の例では，上界と下界に1つずつ袖を追加した配列aを用いています．

  • XMP/Cプログラム
#pragma xmp reflect (a)

#pragma xmp loop on t[i]
for(int i=1;i<15;i++)
  a[i] = (a[i-1] + a[i] + a[i+1])/3;
  • XMP/Fortranプログラム
!$xmp reflect (a)

!xmp loop on t(i)
do i=2, 15
  a(i) = (a(i-1) + a(i) + a(i+1))/3
enddo
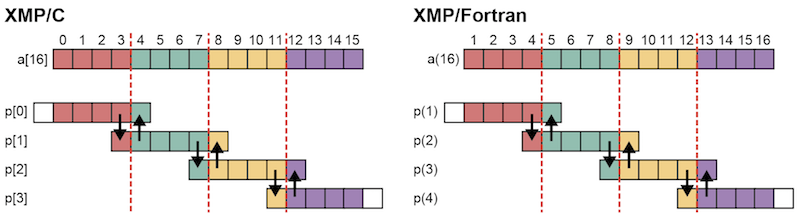
_images/reflect.png

reflect指示文によって，XMP/Cの場合は，ノードp[1]は要素a[4]をノードp[0]の上界の袖領域に，要素a[7]をノードp[2]の下界の袖領域に送信します． また，ノードp[0]は要素a[3]をノードp[1]の下界の袖領域に，ノードp[2]は要素a[8]をノードp[1]の上界の袖領域に送信します．

同様に，XMP/Fortranの場合は，ノードp(2)は要素a(5)をノードp(1)の上界の袖領域に，要素a(8)をノードp(3)の下界の袖領域に送信します． また，ノードp(1)は要素a(4)をノードp(2)の下界の袖領域に，ノードp(3)は要素a(9)をノードp(2)の上界の袖領域に送信します．

13.2.2. 袖更新の幅の指定

reflect指示文では，shadow指示文で宣言された袖に対して更新が行われます． しかし，コードのある部分において，通信量を少なくするため， 袖の特定の要素だけを更新したいことがあります．

袖領域の更新する箇所を指定するには，width節を用います． width節の丸括弧の中にある数字は，コロン左は下界の袖幅，コロン右は上界の袖幅を表します． 下記の例では，上界のみを更新の対象としています．

  • XMP/Cプログラム
#pragma xmp reflect (a) width(0:1)
  • XMP/Fortranプログラム
!$xmp reflect (a) width(0:1)
_images/reflect_width.png

注釈

通信対象となる上界と下界の袖幅が同じ場合，例えば「width(1:1)」の場合は，「width(1)」と簡略化して表現できます．

注釈

特定のノードだけ袖の更新を行う，といったことはできません．

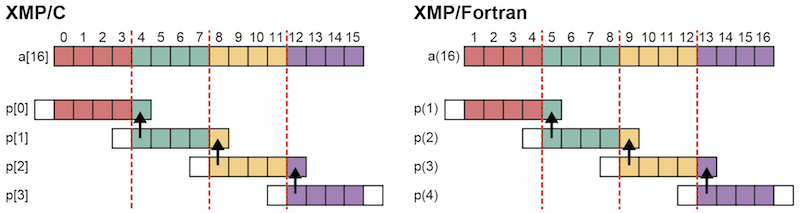
もちろん，shadow指示文で上界しか袖を定義しなかった場合は，width節を利用しなくても上界にしか通信は発生しません． 下図は，上界のみ1つの袖を持つ分散配列aに対してreflect指示文を実行した場合の通信を示しています．

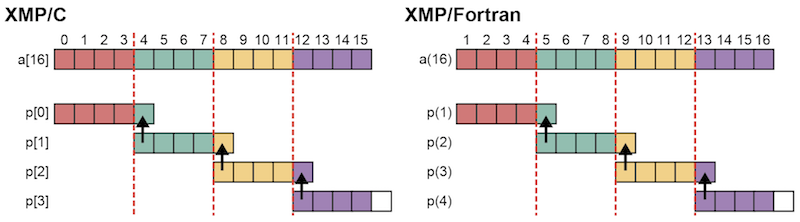
_images/reflect_uneven.png

13.2.3. 巡回領域に対する袖領域の更新

reflect指示文では，最初のノードが持っている下界と，最後のノードが持っている上界の袖については更新されません． しかし，用いている配列が巡回している領域を表す場合は，それらの値がステンシル計算で必要になります．

この更新を行う場合は，periodic修飾子をwidth節に追加します． 下の例では，上界と下界に1つずつ袖を追加した配列aを用いています．

  • XMP/Cプログラム
#pragma xmp reflect (a) width(/periodic/1:1)
  • XMP/Fortranプログラム
!$xmp reflect (a) width(/periodic/1:1)
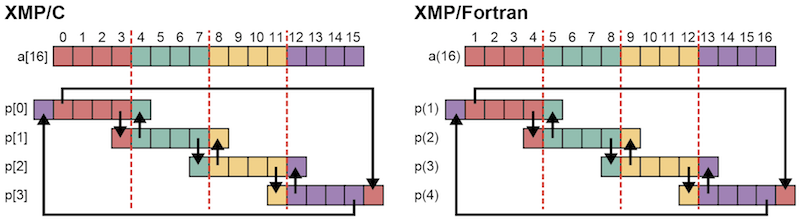
_images/reflect_periodic.png

periodic修飾子によって，通常のreflect通信に加え， XMP/Cの場合は，ノードp[0]は要素a[0]をノードp[3]の上界の袖領域に，ノードp[3]は要素a[15]をノードp[0]の下界の袖領域に送信します． 同様に，XMP/Fortranの場合は，ノードp(1)は要素a(1)をノードp(4)の上界の袖領域に，要素a(16)をノードp(1)の下界の袖領域に送信します．

注釈

上の例の「width(/periodic/1:1)」のように，通信対象となる上界と下界の袖幅が同じの場合は，「width(/periodic/1)」と簡略化して表現できます．

13.3. 多次元の袖領域

shadow指示文とreflect指示文は，多次元分割の配列についても使うことができます． 2次元分割の例を下記に示します．

  • XMP/Cプログラム
#pragma xmp nodes p[3][3]
#pragma xmp template t[9][9]
#pragma xmp distribute t[block][block] onto p
double a[9][9];
#pragma xmp align a[i][j] with t[i][j]
#pragma xmp shadow a[1][1]
   :
#pragma xmp reflect (a)
  • XMP/Fortranプログラム
!$xmp nodes p(3,3)
!$xmp template t(9,9)
!$xmp distribute t(block,block) onto p
real :: a(9,9)
!$xmp align a(j,i) with t(j,i)
!$xmp shadow a(1,1)
   :
!$xmp reflect (a)
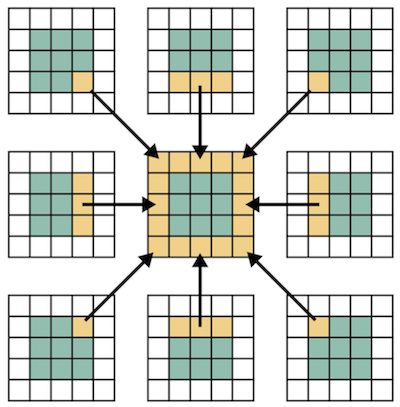
_images/multi1.png

中央のノードは，上下左右と斜め方向に隣接する8ノードから袖のデータを受け取ります． 図では省略していますが，中央のノード以外の袖領域も更新されています．

アプリケーションによっては，斜め方向からのデータが必要ないことがあります． そのような場合，「orthogonal」節をreflect指示文に追加することで，斜め方向からのデータ通信を抑制することができます．

  • XMP/Cプログラム
#pragma xmp reflect (a) orthogonal
  • XMP/Fortranプログラム
!$xmp reflect (a) orthogonal
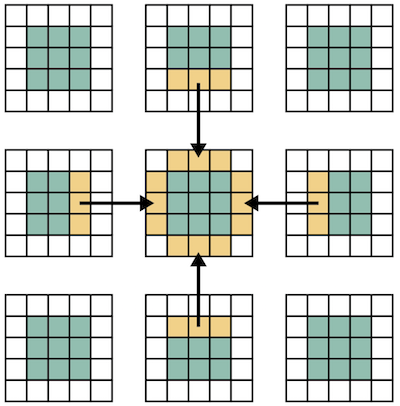
_images/multi_orthogonal.png

注釈

orthogonal節は，2次元以上が分割された配列でしか意味はありません．

また，任意の次元のみに袖領域を追加することもできます．

  • XMP/Cプログラム
#pragma xmp nodes p[3]
#pragma xmp template t[9]
#pragma xmp distribute t[block] onto p
double a[9][9];
#pragma xmp align a[i][*] with t[i]
#pragma xmp shadow a[1][0]
  :
#pragma xmp reflect (a)
  • XMP/Fortranプログラム
!$xmp nodes p[3]
!$xmp template t[9]
!$xmp distribute t[block] onto p
real :: a(9,9)
!$xmp align a(*,i) with t(i)
!$xmp shadow a(0,1)
  :
!$xmp reflect (a)
_images/1of2.png

shadow指示文に指定する配列において，分散していない次元の袖幅には0と記述します．