11. loop指示文

loop指示文は対象のループを並列化する指示文です． そのループ中に現れる分散配列は，下記の条件を満たす必要があります．

1. 繰り返しを跨ぐデータ依存や制御依存がないこと． つまり，ループの繰り返しは，どのような順番で実行しても同じ結果となるようなループであること

  1. 分散配列の要素を持っているノードが，その要素をアクセスすること

11.1. 分散配列へのアクセス

下記のプログラムは，正しいloop指示文とループ文の例です． ループ内でアクセスされる分散配列aのインデックスはiだけなので，条件1をクリアします． また，loop指示文のon節で指定されたテンプレートが持つ各ノードのインデックス情報はループ内の分散配列と同じなので， 条件2もクリアします．

  • XMP/Cプログラム
#pragma xmp nodes p[2]
#pragma xmp template t[10]
#pragma xmp distribute t[block] onto p

int main(){
  int a[10];
#pragma xmp align a[i] with t[i]

#pragma xmp loop on t[i]
  for(int i=0;i<10;i++)
    a[i] = i;

  return 0;
}
  • XMP/Fortranプログラム
program main
!$xmp nodes p(2)
!$xmp template t(10)
!$xmp distribute t(block) onto p
  integer a(10)
!$xmp align a(i) with t(i)

!$xmp loop on t(i)
  do i=1, 10
    a(i) = i
  enddo

end program main
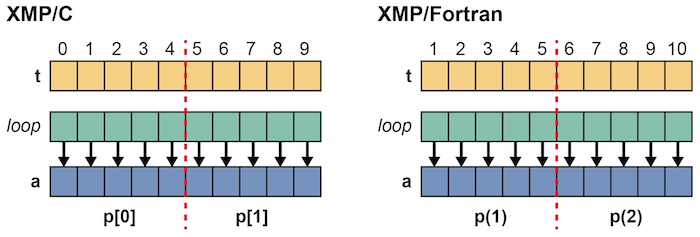
_images/loop1.png

同じプログラムでループの範囲が下記のように小さくなっていたら，並列化できるでしょうか？

  • XMP/Cプログラム（一部分）
#pragma xmp loop on t[i]
  for(int i=1;i<9;i++)
    a[i] = i;
  • XMP/Fortranプログラム（一部分）
!$xmp loop on t(i)
  do i=2, 9
    a(i) = i
  enddo

この場合も，条件1と2をともに満たすため，並列化可能です． XMP/Cでは， p[0]はインデックス1から4を処理し，p[1]は5から8を処理します． 同様に，XMP/Fortranでは，p(1)はインデックス2から5を処理し，p(2)は6から9を処理します．

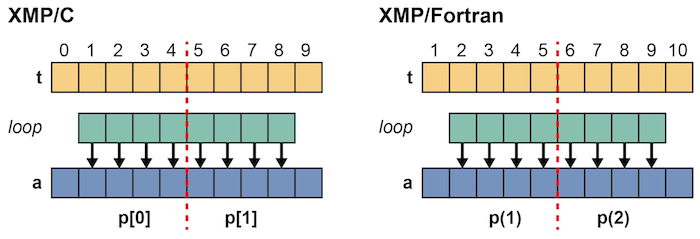
_images/loop2.png

次に，同じプログラムで分散配列のインデックスがずれていたら，並列化できるでしょうか？

  • XMP/Cプログラム（一部分）
#pragma xmp loop on t[i]
  for(int i=1;i<9;i++)
    a[i+1] = i;
  • XMP/Fortranプログラム（一部分）
!$xmp loop on t(i)
  do i=2, 9
    a(i+1) = i
  enddo

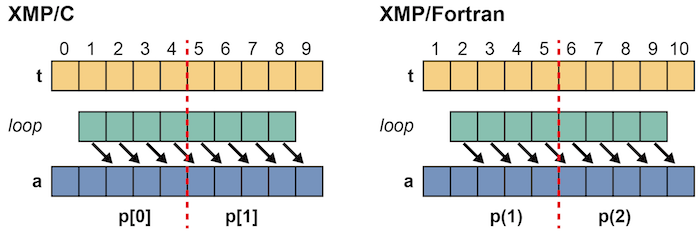
この場合は，条件1は満たしますが，条件2は満たさないため，並列化を行うことができません． XMP/Cでは，p[0]はa[5]をアクセスしようとしますが，p[0]はa[5]を持っていないためです． 同様に，XMP/Fortranでは，p(1)はa(6)をアクセスしようとしますが，p(1)はa(6)を持っていません．

_images/loop3.png

11.2. 集約計算

次の逐次プログラムを使って集約計算について説明します．

  • Cプログラム
#include <stdio.h>

int main(){
  int a[10], sum = 0;

  for(int i=0;i<10;i++){
    a[i] = i+1;
    sum += a[i];
  }

  printf("%d\n", sum);

  return 0;
}
  • Fortranプログラム
program main
  integer :: a(10), sum = 0

  do i=1, 10
    a(i) = i
    sum = sum + a(i)
  enddo

  write(*,*) sum

end program main

上のループをloop指示文だけを使って並列化しようとした場合， ノード毎に変数sumの値が計算されるため， 変数sumの値はノード毎に異なる結果になります．

  • XMP/Cプログラム（未完成．一部）
#pragma xmp loop on t[i]
   for(int i=0;i<10;i++){
     a[i] = i+1;
     sum += a[i];
   }
  • XMP/Fortranプログラム（未完成．一部）
!$xmp loop on t(i)
  do i=1, 10
    a(i) = i
    sum = sum + a(i)
  enddo
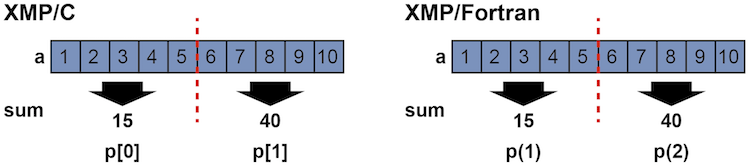
_images/reduction1.png

そこで，loop指示文にreduction節を加えます．

  • XMP/Cプログラム
#include <stdio.h>
#pragma xmp nodes p[2]
#pragma xmp template t[10]
#pragma xmp distribute t[block] onto p

int main(){
  int a[10], sum = 0;
#pragma xmp align a[i] with t[i]

#pragma xmp loop on t[i] reduction(+:sum)
  for(int i=0;i<10;i++){
    a[i] = i+1;
    sum += a[i];
  }

  printf("%d\n", sum);

  return 0;
}
  • XMP/Fortranプログラム
program main
!$xmp nodes p(2)
!$xmp template t(10)
!$xmp distribute t(block) onto p
  integer :: a(10), sum = 0
!$xmp align a(i) with t(i)

!$xmp loop on t(i) reduction(+:sum)
  do i=1, 10
    a(i) = i
    sum = sum + a(i)
  enddo

  write(*,*) sum

end program main

reduction節には集約のための演算子と集約変数を指定します． 上例では加算の演算子を指定しており， この集約計算がノードを跨ぐ総和を求めていることを表現しています．

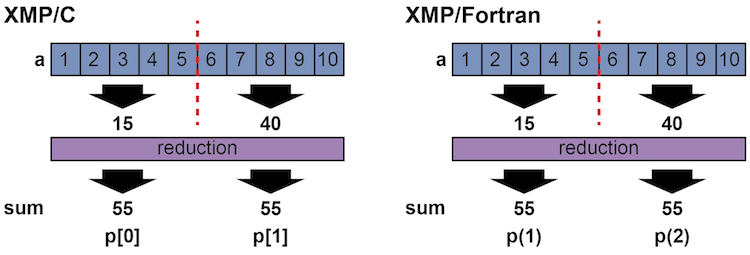
_images/reduction2.png

集約計算に対する演算は，下記の結合則が成り立つ演算に限られます．

  • XMP/Cプログラム
+
*
-
&
|
^
&&
||
max
min
firstmax
firstmin
lastmax
lastmin
  • XMP/Fortranプログラム
+
*
-
.and.
.or.
.eqv.
.neqv.
max
min
iand
ior
ieor
firstmax
firstmin
lastmax
lastmin

注釈

集約変数が浮動小数点型の場合は，計算順序の違いにより，逐次実行と並列実行で結果がわずかに異なる場合があります．

11.3. ネストされたループの並列実行

ネストされたループに対するワークマッピングも，1次元配列と同じように行うことができます．

  • XMP/Cプログラム
#pragma xmp nodes p[2][2]
#pragma xmp template t[10][10]
#pragma xmp distribute t[block][block] onto p

int main(){
  int a[10][10];
#pragma xmp align a[i][j] with t[i][j]

#pragma xmp loop on t[i][j]
  for(int i=0;i<10;i++)
    for(int j=0;j<10;j++)
      a[i][j] = i*10+j;

  return 0;
}
  • XMP/Fortranプログラム
program main
!$xmp nodes p(2,2)
!$xmp template t(10,10)
!$xmp distribute t(block,block) onto p
  integer :: a(10,10)
!$xmp align a(j,i) with t(j,i)

!$xmp loop on t(j,i)
  do i=1, 10
    do j=1, 10
      a(j,i) = i*10+j
    enddo
  enddo

end program main