11. loop construct

The loop directive is used to parallelize a loop. Distributed arrays in such a loop must fulfill the following two conditions:

1. There is no data/control dependence among the iterations. In other words, the iterations of the loop can be executed in any order to produce the same result.
2. An element of a distributed array is accessed only by the node that owns the element.

11.1. Accessing distributed array

The programs below are examples of a right loop directive and a loop statement. The condition 1. is satisfied because i is the only one index of the distributed array a that is accessed within the loop, and the condition 2 is also satisfied because the indices of the template in the on clause of the loop directive is identical to that of the distributed array.

• XMP/C program

#pragma xmp nodes p[2]
#pragma xmp template t[10]
#pragma xmp distribute t[block] onto p

int main(){
  int a[10];
#pragma xmp align a[i] with t[i]

#pragma xmp loop on t[i]
  for(int i=0;i<10;i++)
    a[i] = i;

  return 0;
}

• XMP/Fortran program

program main
!$xmp nodes p(2)
!$xmp template t(10)
!$xmp distribute t(block) onto p
  integer a(10)
!$xmp align a(i) with t(i)

!$xmp loop on t(i)
  do i=1, 10
    a(i) = i
  enddo

end program main

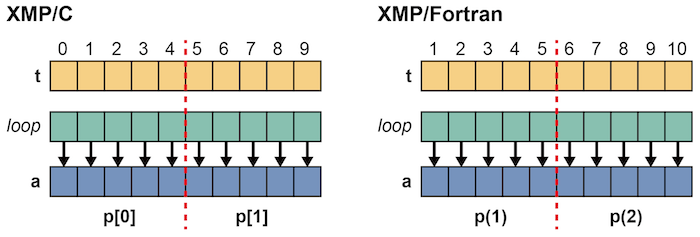
Is it possible to parallelize the below loops whose bounds are shrunk?

• XMP/C program

#pragma xmp loop on t[i]
  for(int i=1;i<9;i++)
    a[i] = i;

• XMP/Fortran program

!$xmp loop on t(i)
  do i=2, 9
    a(i) = i
  enddo

In this case, the conditions 1 and 2 are satisfied and therefore it is possible to parallelize them. In XMP/C, p[0] processes the indices from one to four and p[1] from five to eight. In XMP/Fortran, p(1) processes the indices from two to five and p(2) from six to nine.

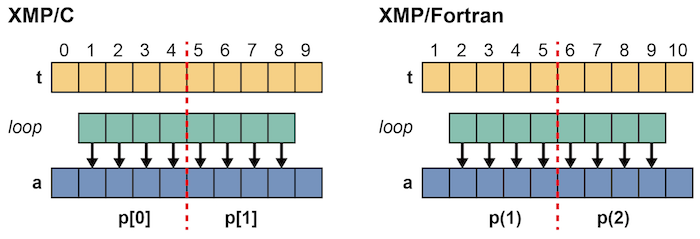
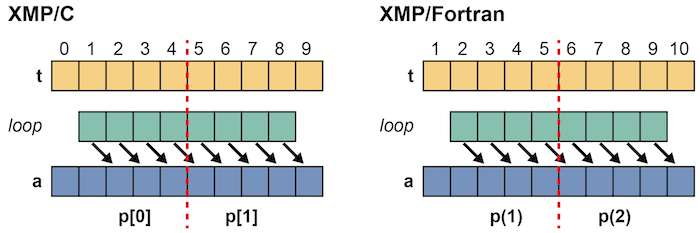
Next, is it possible to parallelize the below loops in which the index of the distributed array is different?

• XMP/C program

#pragma xmp loop on t[i]
  for(int i=1;i<9;i++)
    a[i+1] = i;

• XMP/Fortran program

!$xmp loop on t(i)
  do i=2, 9
    a(i+1) = i
  enddo

In this case, the condition 1 is satisfied but 2 is not, and therefore it is not possible to parallelize them. In XMP/C, p[0] tries to access a[5] but does not own it. In XMP/Fortran, p(1) tries to access a(6) but does not own it.

11.2. Reduction computation

The serial programs below are examples of the reduction computation.

• C program

#include <stdio.h>

int main(){
  int a[10], sum = 0;

  for(int i=0;i<10;i++){
    a[i] = i+1;
    sum += a[i];
  }

  printf("%d\n", sum);

  return 0;
}

• Fortran program

program main
  integer :: a(10), sum = 0

  do i=1, 10
    a(i) = i
    sum = sum + a(i)
  enddo

  write(*,*) sum

end program main

If the above loops are parallelized only with the loop directive, the value of the variable sum varies from node to node because it is calculated on each node.

• XMP/C program

#pragma xmp loop on t[i]
   for(int i=0;i<10;i++){
     a[i] = i+1;
     sum += a[i];
   }

• XMP/Fortran program

!$xmp loop on t(i)
  do i=1, 10
    a(i) = i
    sum = sum + a(i)
  enddo

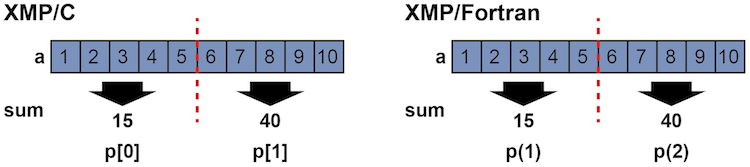
Then, add the reduction clause to the loop directive.

• XMP/C program

#include <stdio.h>
#pragma xmp nodes p[2]
#pragma xmp template t[10]
#pragma xmp distribute t[block] onto p

int main(){
  int a[10], sum = 0;
#pragma xmp align a[i] with t[i]

#pragma xmp loop on t[i] reduction(+:sum)
  for(int i=0;i<10;i++){
    a[i] = i+1;
    sum += a[i];
  }

  printf("%d\n", sum);

  return 0;
}

• XMP/Fortran program

program main
!$xmp nodes p(2)
!$xmp template t(10)
!$xmp distribute t(block) onto p
  integer :: a(10), sum = 0
!$xmp align a(i) with t(i)

!$xmp loop on t(i) reduction(+:sum)
  do i=1, 10
    a(i) = i
    sum = sum + a(i)
  enddo

  write(*,*) sum

end program main

An operator and target variables for reduction are specified in a reduction clause. In the above examples, a “+” operator is specified for the reduction computation to produce a total sum among nodes.

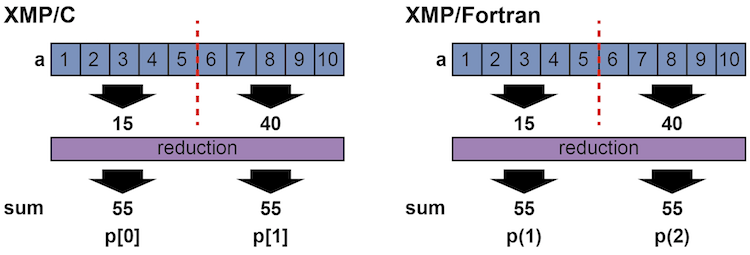
Operations that can be used in a reduction computation are limited to the following associative ones.

• XMP/C program

+
*
-
&
|
^
&&
||
max
min
firstmax
firstmin
lastmax
lastmin

• XMP/Fortran program

+
*
-
.and.
.or.
.eqv.
.neqv.
max
min
iand
ior
ieor
firstmax
firstmin
lastmax
lastmin

Note

If the reduction variable is a type of floating point, the difference of the order of the executions can make a little bit difference between serial and parallel executions

11.3. Parallelizing nested loop

Parallelization of nested loops can be specified similarly for a single loop.

• XMP/C program

#pragma xmp nodes p[2][2]
#pragma xmp template t[10][10]
#pragma xmp distribute t[block][block] onto p

int main(){
  int a[10][10];
#pragma xmp align a[i][j] with t[i][j]

#pragma xmp loop on t[i][j]
  for(int i=0;i<10;i++)
    for(int j=0;j<10;j++)
      a[i][j] = i*10+j;

  return 0;
}

• XMP/Fortran program

program main
!$xmp nodes p(2,2)
!$xmp template t(10,10)
!$xmp distribute t(block,block) onto p
  integer :: a(10,10)
!$xmp align a(j,i) with t(j,i)

!$xmp loop on t(j,i)
  do i=1, 10
    do j=1, 10
      a(j,i) = i*10+j
    enddo
  enddo

end program main